Ocelový vazník v dřevěném krovu
Zadání
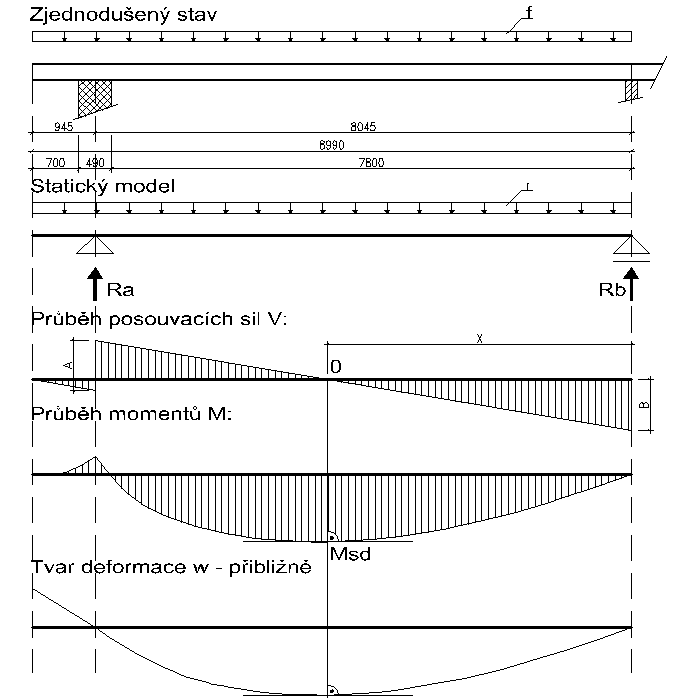
Navrhněte ocelový vazník nesoucí dřevěný krov RD z uzavřeného profilu třídy 1, navrhněte profil Jä. Vzhledem k uložení počítejte pouze zatížení ohybovým momentem. Posuďte na MSÚ a MSP.
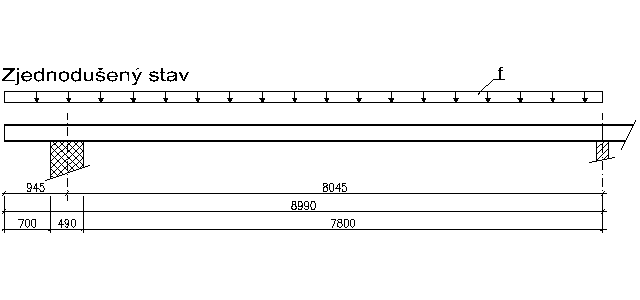
Skladba střešního pláště viz. tabulka stálého zatížení, sněhová oblast - město Jičín. Z nahodilých zatížení zohledněte pouze zatížení sněhem. Zatěžovací šířka trámu 3,055m, viz. obr. 2.
Výpočet zatížení
Zatěžovací šířka
Zatížení stálé
| MATERIÁL | ZATÍŽENÍ [kN/m2] |
| Střešní krtytina - tašky Bramac 43kN/m2 | 0,43 |
Dřevěný trám Ø1 ks/bm 200x140 mm ρv =650 kg/m3. 0,2 . 0,14 . 0.65 | 0,02 |
Sdk 15mm;0,65kN/m2 Podbití-dřevovl. deska 15mm;0,65 kN/m2 0.65 . 2x15mm | 0,02 |
| Tepelná izolace Rockwool 240mm | 0,00 |
| gk | ∑=0.47 kN/m2 |
Převod na liniové zatížení vazného trámu:
Gk1= zš . gk = 0,47 .3,055 = 1,44 kN/m2
Připočtení vlastní tíhy ocelového vazníku:
Odhad profilu Jä 250x150x8 ... 46,5 kg/m2, Gk2=0,465 kN/m2
Celkem stálé liniové zatížení vazníku:
Gk = Gk1 + Gk2 =1,44 + 0,465 = 1,91 kN/m2
Zatížení nahodilé - sněhem
Viz. sněhová mapa Jičín s0 = 1.0 kN/m2
sk,ploš = s0 . 1,0 . 1,0 = 1,0 kN/m2
Přepočet plošného zatížení sněhem na liniové:
sk = Qk = sk,ploš . zš = 1,0 . 3,055 = 3,055 kN/m2
Pro naše potřeby nemusíme počítat několik zatěžovacích stavů - převislý konec vazníkíku má zanedbatelnou délku a výsledný moment by prakticky neovlivnilo poloviční zatížení sněhem. V případě delšího konce ovšem je nutno posoudit všechny zatěžovací stavy a konstrukci navrhnout na nejnepříznivější možné stavy vnitřních sil.
Kombinace zatížení:
fd = γG . Gk + γQ . Qk = 1,2 . 1,91 + 1,35 . 3,06 = 6.42 kN/m2
Výpočet vnitřních sil
(schema viz. obrázek níže)
Pro přehlednost si vše rozkreslíme rozfázovaně.
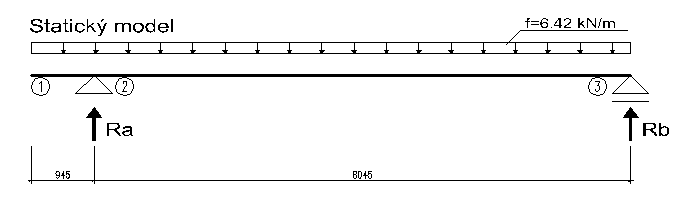
Výsledné reakce od liniového zatížení:
Momentová podmínka k bodu 2:
6,42 /2 . (8,0552 - 0,9452) = 8,055 . Rb
Rb = 25,50 kN
Momentová podmínka k bodu 3:
6,42 . 9,02/2 = 8,055 . Ra
RA = 32.28 kN
Kontrola ve svislém směru:
Ra + Rb = f . 9
32,28 + 25,50 =6,42 . 9,0
57,78 = 57,78 , platí, výsledek je správný
Průběhy vnitřních sil
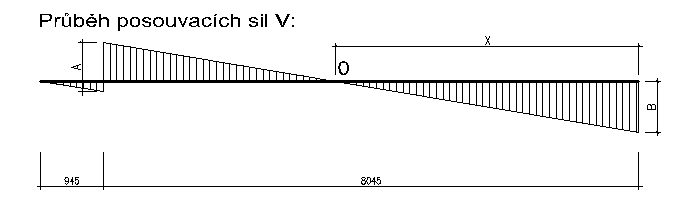
Posouvací síla Vz (též značená Qz)
interval 1-2:
Vz = -fd . x
Vz2 = -6,42 . 0.945 = 6,07 kN
interval 3-2:
Vz = - Rb + fd . x = -25,50 + 6,42 . x
Vz2 = - 25,50 + 6,42 . 8,055 = 19,43 kN
Ohybový moment My
Najití maxim momentu (definice :Vy = -dMy / dx), hledáme lokání maxima, tedy moment zderivujeme a položíme roven nule. Více matematiky potřebovat nebudeme, ač se znalost matematiky vždy zužitkuje.
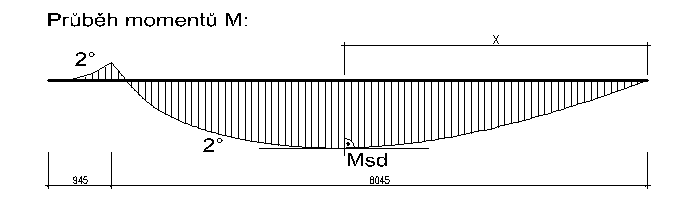
Interval 1-2:
My = - fd . x2/2
My2 = 6,42 . 0,9452/ 2 = 2,87 kNm
Interval 3-2:
My = Rb - fd . x2/2
zjištění maxima - vzdálenost x od bodu 3:
Vz = 0 = Rb - fd . x
x = 25,50 / 6,42 = 3.972 m
a tedy:
Mmax = 25,50 . 3,972 - 6,42 . 3,9722 / 2 = 50,64 kNm
My2 = 6,42 . 0,9452/ 2 = 2,87 kNm
Předběžný návrh profilu tř. 1.
Budeme navrhovat pouze pro nosník elasticky přetvořen (tj. požadavek, jinak zásadně průřezy tř. 1 navrhujeme zásadně platicky).
Wy,el,min = Msd . γM / fy = 50,64 . 1,15 / (235 . 103) = 247,8 cm3
fyzikální konstanty viz.
Pevnost konstrukční ocel a Ocel - návrhové hodnoty materiálových konstant
Návrh profilu z katalogu Ferona:
Profil Jä 200x150x8
zde jsou specifikace:
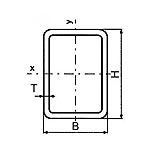
| Výška profilu | H | 200 mm |
| Šířka profilu | B | 150 mm |
| Tloušťka profilu | T | 8,0 mm |
| Hmotnost | M | 40,23 kg/m |
| Plocha průřezu | A | 51,24 cm2 |
| Kvadratický moment průřezu | Ixx | 2829 cm4 |
| Kvadratický moment průřezu | Iyy | 1820 cm4 |
| Poloměr kvadratického momentu průřezu | ixx | 7,43 cm |
| Poloměr kvadratického momentu průřezu | iyy | 5,96 cm |
| Pružný modul průřezu | Welxx | 283 cm3 |
| Plastický modul průřezu | Wplxx | 344 cm3 |
| Plastický modul průřezu | Wplyy | 283 cm3 |
| Pružný modul průřezu | Welyy | 243 cm3 |
| Polární moment průřezu | It | 3665 cm4 |
| Polární modul průřezu | Ct | 396 cm3 |
| Plocha povrchu na 1 m délky | As | 0,666 m2/m |
| Jmenovitá délka na 1 t | 24,9 m | |
| Mezní úchylka H | ±0,8 % | |
| Mezní úchylka B | ± 0,8 % | |
| Mezní úchylka T | ±0,5 mm | |
| Vydutost strany | x1 | nejvýše 0,8 %, nejméně 0,5 mm |
| Vypuklost strany | x2 | nejvýše 0,8 %, nejméně 0,5 mm |
| Kolmost stran | 90° ± 1° | |
| Tvar vnějšího zaoblení | C1, C2 | 2,0T až 3,0T |
| Zkroucení | V | 2 mm plus 0,5 mm/m délky |
| Mezní úchylka přímosti na 1 m délky | max 3 mm |
Posouzení
Mezní stav únosnosti - MSÚ
MRD,el = Wy,el . fy / jM1 = 283 . 355 . 10-3 / 1,15 = 87.3 kNm
pro zajímavost též:
MRD,pl = Wy,pl . fy / jM1 = 344 . 355 . 10-3 / 1,15 = 106.1 kNm
Posouzení : MRD,el=87.3 kNm > MSD=50.64kNm .. průřez má dostatečnou únosnost - vyhovuje
Mezní stav použitelnosti - MSP
Průhyb vzhledem k schematu nelze počítat jednoduchým vzorcem pro prostý nosník ( "δ=5 . fD . L4 / [384 . E .Iy] "), ale musíme vycházet z rovnice ohybové čáry:
w''(x) = - My(x) / (E . Iy)
Interval 3-2:
EIy = konst. = A
A . w''(x) = - (2,6 . x2 -
clanek dodelavam.... zachvili bude..
| Únosnost drátu - ocelového kruhového prutu v tahu. | MSÚ (mezní stav únosnosti) |
| Hmotnost běžného metru betonářské oceli | |
| Kari sítě 500S - výrobní progam | Hmotnosti, rozčlenění, info,.. |
| Hmotnosti U profilů (běžný metr) | U50 - U400 |
| Hmotnosti I profilů (běžný metr) | I80 - I360 |
| Adekvátní EN oceli k českým vysokopevnostním ocelím | |
| Výpočet únosnosti šroubů pro opláštění dle ENV 1993-1-3, excel | .xls automatický výpočet |
| MSÚ oceli - Tah, prostý tlak | Podmínka únosnosti |
| Nejmenší výšky koutových svarů ocelových konstrukcí | Jednovrstvé koutové svary |
| Součinitele materiálu γM pro ocel, třídy průřezů | |
| Termíny a značky ocelových konstrukcí ČSN P ENV 1991-1-1 | Užitečné info pro začátek v oceli |
| Mez kluzu a pevnosti pro šrouby | Šrouby 4.6, 4.8, 5.6, 5.8, 6.8, 8.8, 10.9 |
| Ocel - návrhové hodnoty materiálových konstant | Modul pružnosti, modul pružnosti ve smyku, koef. tepelné roztažnosti, objemová hmotnost, Poissonův součinitel |
| Pevnost konstrukční oceli | fy, fu |
Přečteno:14888
Autor: David Mizera
Komentáře (5)
- Nový Komentářcau,
trochu pitomost, to zadani, ne? :) nemyslis nahodou vaznici? ;)